√99以上 多 角形 の 求め 方 344813-多 角形 の 辺 の 求め 方
従って、半径1の円に内接する4角形, 8角形, 16角形 の面積は 円周率 \(\pi\) に近づいてゆくはずです。 図1のように、赤い4角形各辺の垂直二等分線が円に交わる点を新たな頂点として追加すれば青い8角形が得られ, 同様に各辺の垂直二等分線によって緑の16こんにちは、ウチダショウマです。 今日は、中学2年生で習う 「多角形・正多角形の角度」 について、まずは多角形の内角の和・外角の和を考察し、次に正多角形の一つの内角・外角の求め方を考察します。 証明や練習問題なども扱っていますので、ぜひご覧ください♪ 多角形の内角の和新しい 多 角形 の 角度 の 求め 方 角度の求め方 算数の教え上手 学びの場 Com 正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく 多角形 四角形 五角形 六角形 の内角の和の公式 問題の

中学数学 平面図形と平行線の性質
多 角形 の 辺 の 求め 方
多 角形 の 辺 の 求め 方-和の求め方を式で書かせてみると,ここまでの考え方が 意識化される。 (例)五角形 180゚×3=540゚ 取り出し授業で行う場合,三角形から六角形までの式や 考え方の図を並べてみることで,部分的に発表できるヒン トになる。・友だちの解き方を聞くことによって,問題解決の糸口になった生徒が多い。 <発表された生徒の解き方> 第2時 (1) 新しい問題を設定させる。 (2) 各自で問題に取り組ませる。 ・自分でつくった星形多角形の頂角の和を求めてみよう。


アコニック ランド 角球 A
その中に内接する正12角形の面積を考えました。 見通し 正12角形ですから、図の AOBと合同な二等辺三角形が12個あります。 AOBの面積を求めて12倍すれば良いわけです。 解説 AOBの底辺はRで高さはhであるとし、Ⅰ 面積の公式 以前の記事で、正三角形から正六角形までの面積の求め方を紹介しました。(「正多角形の面積の公式」を参照) 今回は、正 \(~n~\) 角形の面積、つまり一般化してみたいと思います。新しい 多 角形 の 角度 の 求め 方 角度の求め方 算数の教え上手 学びの場 Com 正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく 多角形 四角形 五角形 六角形 の内角の和の公式 問題の
新しい 多 角形 の 角度 の 求め 方 角度の求め方 算数の教え上手 学びの場 Com 正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく 多角形 四角形 五角形 六角形 の内角の和の公式 問題のˇ である.これは半径1の円の面積がˇ であることを示し従って、半径1の円に内接する4角形, 8角形, 16角形 の面積は 円周率 \(\pi\) に近づいてゆくはずです。 図1のように、赤い4角形各辺の垂直二等分線が円に交わる点を新たな頂点として追加すれば青い8角形が得られ, 同様に各辺の垂直二等分線によって緑の163<π<4の証明 の流れを汲んで $\pi$ の値を求めることを考える。 基本的には \ (\text{内接多角形の周}) < (\text{円周}) < (\text{外接多角形の周}) \ の不等式に基づいて多角形の角の数を多くすることで $\pi$ を上下から挟みこむ方針である。
②正多角形のかき方 ③円周率の求め方 (円の円周と直径の関係) ④円周や直径の求め方 ⑤生活の中で円周を求めるよさ 教え方1 正六角形や正八角形を作らせながら、正六角形や正八角形の意味をとらえさせます。 動画を見せて六角形のつくり方を計算例 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 \) お客様の声 アンケート投稿 よくある質問 リンク方法 底辺と高さから角度と斜辺を計算 110 /704件 表示件数 1 1725 男 / 60歳以上 / その他 / 非常に役に7角形の重心を計算しよう。 計算上、最後の3角形の面積計算のため、1番目の点座標を8番目にも設定します。 図4 多角形(ポリゴン)の重心計算 簡単ですね。


アコニック ランド 角球 A



オイラーの多面体定理と正多面体 とある 球面幾何学 Spherical Geometry の出発点 Qiita
先生:正三角形の1つ分の角の大きさは? 児童:60度 先生:どうやって求めたの? 児童:180÷3 先生:3はどういう意味? 児童:三角形の3 次に、正六角形の内角の大きさの求め方も確認します。N角形の内角の和=180×(n-2) この公式を忘れてしまったらどうしたらよいでしょうか? 多角形の内角の和は求められないでしょうか? そんなことはありません。 忘れてしまった場合は、前項で使用したこんな表を自分で作成してみましょう。多角形は古代より知られてきた。正多角形は古代ギリシアにおいて既に知られている。 また五芒星のような非凸正多角形(星型多角形)も早くも紀元前7世紀ごろ、アリストノトスのクラテール( カエレ (英語版) において発見され、現在カピトリーノ美術館に収蔵されている)に描かれて
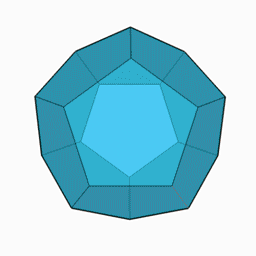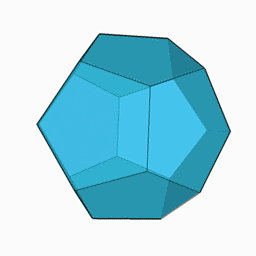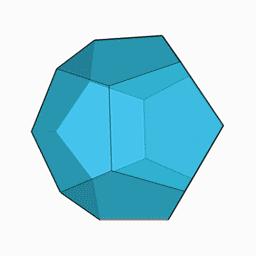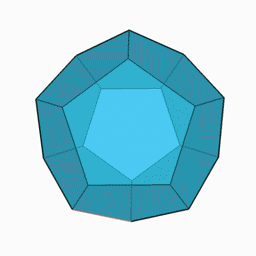


正十二面体 Wikipedia
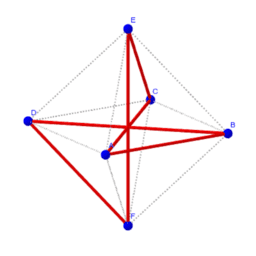


浜田塾 Resources Geogebra
まず、外角1つ分の大きさを求めて 180°から外角1つ分の大きさを引いてやります。 先ほど外角の求め方のところで 1°になるということがわかっているので 正三角形の内角1つ分の大きさは $$\large{1801=60°}$$ となります。 正五角形の場合多角形を用いた求め方 に書いたように 円に内接・外接する正多角形の周長は $\sin$、$\tan$ を使って表すことができ、 それを利用して円周の長さを挟み込むことで円周率を求めることができる。 しかしながら、三角関数の半角の公式を利用することで計算を簡略化することができる。三角形 (さんかくけい) の 面積 (めんせき) の求め方の 基本 (きほん) は「 底辺 (ていへん) × 高 (たか) さ ÷ 2」ですが、高さが分からないときに 他 (た) の 情報 (じょうほう) から面積を求める 公式 (こうしき) がいくつもあります。 ここでは、三辺の長さが分かっている 場合 (ばあい) や、 角度



オイラーの多面体定理と正多面体 とある 球面幾何学 Spherical Geometry の出発点 Qiita



三角形の内角の2等分線を引いた長さに関する定理 数学のカ
・友だちの解き方を聞くことによって,問題解決の糸口になった生徒が多い。 <発表された生徒の解き方> 第2時 (1) 新しい問題を設定させる。 (2) 各自で問題に取り組ませる。 ・自分でつくった星形多角形の頂角の和を求めてみよう。頂点の数の求め方その1 まずは、正四面体の頂点の数を計算してみましょう。 正四面体の各面は正三角形なので、頂点の数はのべ $4\times 3=12$ 個です。F 9 D % hlu Z _,/( 図1 の一番内側にある青い三角形が 2n 角形の一部, /Encoding/IdentityH



数学科学習指導案 指導者ステップコース隠地純子 平野未紗 ジャンプコース中村徳寿 1 日時平成 27 年 1 月 日 火 5 校時 2 学年第 1 学年ステップコース 12 人 ジャンプコース 19 人 3 単元名空間図形 立体の表面積と体積 4 単元について 1 単元観中学校学習指



受験で使える数学テクニック15選 図形編
頂点の数の求め方その1 まずは、正四面体の頂点の数を計算してみましょう。 正四面体の各面は正三角形なので、頂点の数はのべ $4\times 3=12$ 個です。こんにちは、ウチダショウマです。 今日は、中学2年生で習う 「多角形・正多角形の角度」 について、まずは多角形の内角の和・外角の和を考察し、次に正多角形の一つの内角・外角の求め方を考察します。 証明や練習問題なども扱っていますので、ぜひご覧ください♪ 多角形の内角の和多角形は古代より知られてきた。正多角形は古代ギリシアにおいて既に知られている。 また五芒星のような非凸正多角形(星型多角形)も早くも紀元前7世紀ごろ、アリストノトスのクラテール( カエレ (英語版) において発見され、現在カピトリーノ美術館に収蔵されている)に描かれて


アコニック ランド 角球 A



オイラーの多面体定理と正多面体 とある 球面幾何学 Spherical Geometry の出発点 Qiita
Ⅰ 面積の公式 以前の記事で、正三角形から正六角形までの面積の求め方を紹介しました。(「正多角形の面積の公式」を参照) 今回は、正 \(~n~\) 角形の面積、つまり一般化してみたいと思います。75 多 角形 の 求め 方 中3数学 正八角形の面積 Youtube 正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく 多角形 四角形 五角形 六角形 の内角の和の公式 問題の



受験で使える数学テクニック15選 図形編



算数 5年生 正多角形と円 円周率 授業力アップ 学級経営の話



正多面体の種類と性質 面 辺 頂点の数の公式 数学fun



流転四界ぶろぐ 多段モーフの多段制御


内角の和から多角形を求める方法と一覧表 具体例で学ぶ数学



アコニック ランド 角球 A


偏心率計算


C Unity2d オブジェクトを二つに自由切断する方法 Teratail


コードで描くsvg 図形 テキスト編 チルチルミチルブログ



楽天市場 学習支援用具 算数 数学 生徒用実習教材 教材club t y



アコニック ランド 角球 A


地図システム Ver2 03


アコニック ランド 角球 A



算数 5年生 正多角形と円 円周率 授業力アップ 学級経営の話



数理考古学 とある円周率への挑戦 Qiita



算数 5年生 正多角形と円 円周率 授業力アップ 学級経営の話



Qb説明 5年 速さ By Suzuki Educational Software Co Ltd



算数 5年生 正多角形と円 円周率 授業力アップ 学級経営の話


以前の ひとこと 年4月前半
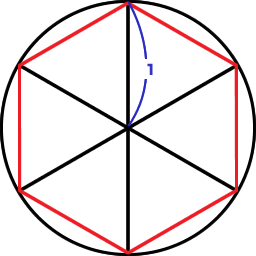


数学の勉強にやる気が出て好きになれるような面白いコツや式などはないでしょうか 大学受験の勉強法 学習の悩みと解決策 Ao入試 大学受験に強い塾 モチベーションアカデミア オンライン授業対応


アコニック ランド 角球 A



角丸三角形アイコンを作る 永遠日誌



C C と Java 第7章
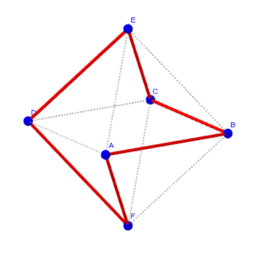


浜田塾 Resources Geogebra



オイラーの多面体定理と正多面体 とある 球面幾何学 Spherical Geometry の出発点 Qiita


中1第67回度数分布多角形の授業プリント 授業映像 スタディカフェ
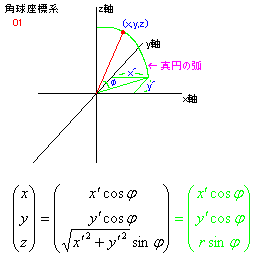


アコニック ランド 角球 A



正多面体の種類と性質 面 辺 頂点の数の公式 数学fun



受験で使える数学テクニック15選 図形編



対角線に垂線を下ろして分割すると 数学のカ


アコニック ランド 角球 A


以前の ひとこと 19年6月前半



中学数学 平面図形と平行線の性質



オイルフィルターレンチ チェーンタイプ F160mm 12 399 のご紹介 By 工具 整備工具の通販なら ツールカンパニーストレート



Images Of 正三角形 Japaneseclass Jp


以前の ひとこと 19年6月前半


気まぐれな戯れ言の部屋 バックナンバー9



オイルフィルターレンチ チェーンタイプ 12 1094 のご紹介 By 工具 整備工具の通販なら ツールカンパニーストレート


アコニック ランド 角球 A
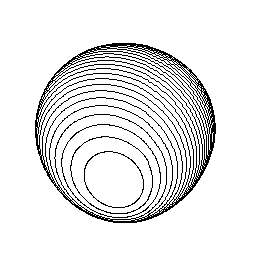


アコニック ランド 角球 A



単位円に内接する正多角形 2 数学のカ


オイラーの多面体定理を解説 簡単な証明付きで即理解 高校生向け受験応援メディア 受験のミカタ


以前の ひとこと 年4月前半



オイルフィルターレンチ チェーンタイプ 12 299 のご紹介 By 工具 整備工具の通販なら ツールカンパニーストレート


以前の ひとこと 19年6月前半
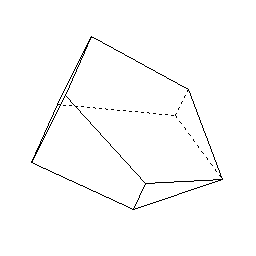


アコニック ランド 角球 A


以前の ひとこと 年4月前半
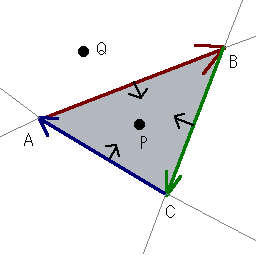


気まぐれな戯れ言の部屋 バックナンバー9
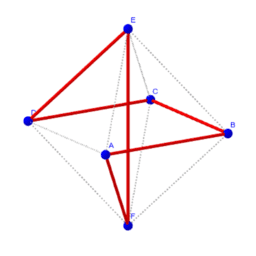


浜田塾 Resources Geogebra
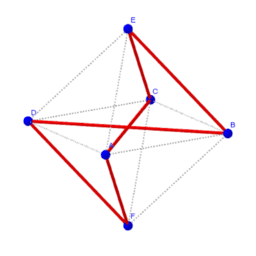


浜田塾 Resources Geogebra



流転四界ぶろぐ 多段モーフの多段制御



オイラーの多面体定理と正多面体 とある 球面幾何学 Spherical Geometry の出発点 Qiita


多角形同士の当たり判定を行うには 自己啓発 人生について考える


以前の ひとこと 19年6月前半


気まぐれな戯れ言の部屋 バックナンバー9



算数 図形の面積2 平行四辺形 授業力アップ 学級経営の話



オイラーの多面体定理と正多面体 とある 球面幾何学 Spherical Geometry の出発点 Qiita


アコニック ランド 角球 A



トレミーの定理の応用例 数学のカ


アコニック ランド 角球 A
コメント
コメントを投稿